Rendering real-time physics: video game physics engines

Augmented reality in action – a fast, portable and realistic physics engine is needed to calculate the collisions with complex surfaces in the real world (Lightship SDK)
Curiosity has recently led me down the road of extended reality (XR), a catch-all term encompassing: Augmented Reality (AR), Mixed Reality (MR) and Virtual Reality (VR). Development of XR experiences interestingly uses much of the same tooling used to create video games, often using game engines like Unity to build and leverage technology in order to create virtual environments.
Modern game engines are becoming ever more wieldy, enabling developers to pursue more ambitious ideas on increasingly resource-constrained platforms. A game engine is a software package with a set of well-integrated functionalities for game development, a typical modern game engine is likely to provide: a rendering engine for 2D/3D graphics, sound, scripting, animation, artificial intelligence (AI), networking, streaming, memory management and notably a physics engine for simulating the physical interactions within the generated virtual environment.
Physics engines are primarily used to abstract away the complexity of codifying the laws of mechanics in a virtual world from scratch. Those used in game engines often go a step further, providing developers a highly interoperable solution with other functionalities such as a graphics and sound modules. Originating from a need to process highly specialised scientific simulations, for example ballistics profiling for the US Army being an early use-case, modern game-oriented physics engines instead use real-time processing. While unlocking the ability to create highly immersive games that appear perceptually correct, the physical interactions generated are not always true to life. Modern engines struggle with the common computer science adage of a time complexity trade-off, simplifying and approximating physics in favour of a responsive real-time experience.
How do real-time physics engines work?
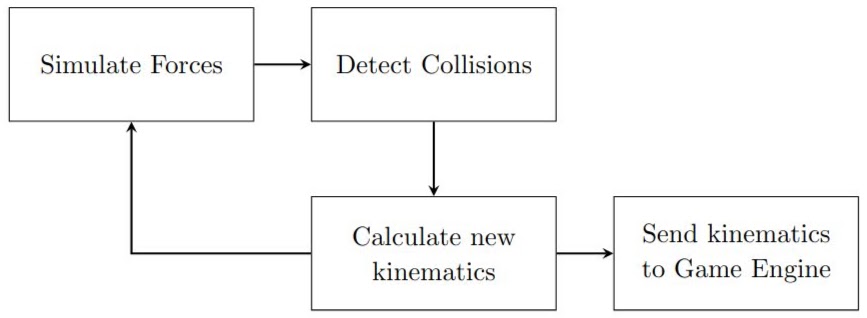
Simplified update loop of a physics engine
At the most basic level a real-time physics engine works on a cyclical read ⟷ update loop, typically:
- Assess current forces on all entities in the scenegraph
- Calculate kinematics for the next timestep
- Update entities’ positions and velocities.
Doing so at a high enough frequency simulates the application of force on an entity in real-time and when done in parallel with multiple entities, provides the illusion of global physics (see update loop diagram). Under the same force entities kinematic behaviours would then vary depending on their material properties and entity type, e.g. rigid-body, soft-body, cloth, fluid.
Although the exact architecture and physical laws implemented vary between engines the equations of motion are the most important and almost universally relied on. The key equation being Newton’s Second Law: $$\vec{F} = m \times \vec{a}$$
Where $\vec{F}$ is force in the x, y, z axes, $m$ the mass of the entity and $\vec{a}$ the acceleration in each respective axis. When extended to rotational motion i.e. angle, angular velocity and angular acceleration:
$$\vec{M} = I \times \vec{\alpha}$$
Where $\vec{M}$ is the moment about the x, y, z directions, $I$ the mass moment of inertia and $\vec{\alpha}$ the angular acceleration in each respective direction. On each loop of the physics engine the instantaneous translational and rotational kinematics of an entity is updated by:
- Identifying all moments and forces acting on each entity in the scenegraph.
- Take the vector sum of all moments and forces for each entity.
- Use the described equations of motion for translational and angular acceleration.
- Integrate the acceleration with respect to time to find the translational and angular velocity.
- Integrate the velocity with respect to time to find the translational and angular displacement.
Where engines differ is by how they complete the above steps and although there exist many subtleties between engines, time is spent to highlight two of the most common variances for the reader’s benefit: 1) The numerical solvers used to integrate an entity’s kinematic properties 2) The way collisions between entities are handled.
Further reading: C. Ericson’s, Real-time collision detection
Numerical Solver
Once the sum of moments and forces for an entity is calculated and equations of motion applied, the engine must integrate the equations with respect to time, thus generating the entity’s kinematics. As a computer cannot approach these integrals analytically they must be solved with computational methods. Some of the most common include:
- Euler Method
- Verlet Method
- Runge-Kutta Method
Each varying in time complexity, auxiliary memory complexity and convergence rate upon an optimal solution, meaning it is crucial the solver use is calibrated to its use-case. Much of the work around improving solvers leverages the discipline of computational methods.
Collision Handling
Collision handling encompasses collision detection algorithms, entity bounding volumes and the mathematics of momentum transfer between colliding entities. Similarly, the approach to each component will vary between engines, for example, the type of bounding volumes used can vary depending on the accuracy expected and compute the engine can leverage. Typical volumes in order of increasing accuracy and complexity might include:
- Spheres
- Axis-Aligned Bounding Boxes (AABB)
- Oriented Bounding Boxes (OBB)
- Convex Hull
These collisions are registered by the engine’s collision detection algorithm which is run during the physics engine loop. The Gilbert-Johnson-Keerthi (GJK) algorithm is one of the commonly used algorithms for achieving precise low false-positive collisions, relying on an iterative method of computing the Euclidean distance between two convex sets in an n-dimensional space.
Further reading: P. Terdiman, Memory-optimized bounding-volume hierarchies
Physics engines found in modern games
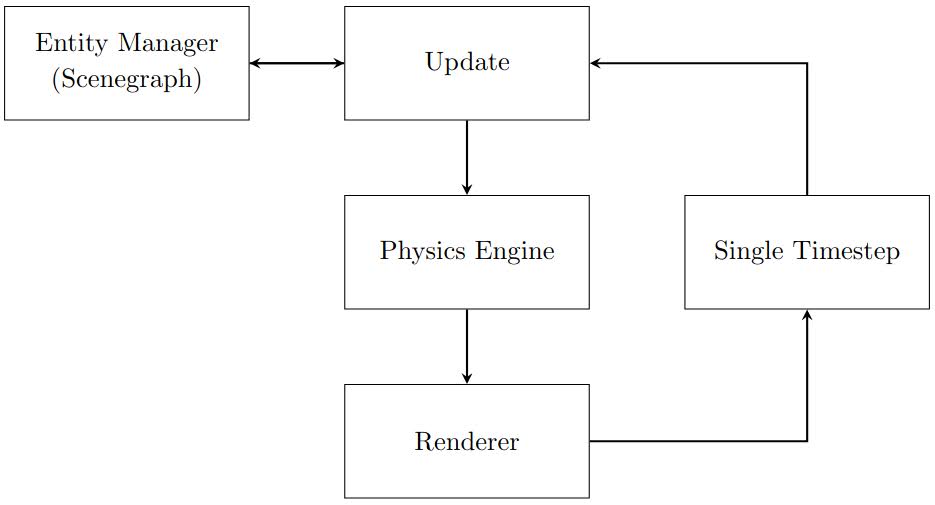
Physics engines are called in each update of a frame (e.g. at 60 Hz+)
Of the many general-purpose physics engines that exist, many do so in the context of a modern game engines. This is typically because the the physics engine passes calculated kinematics information of entities in the scenegraph directly to the renderer to visualise, creating the illusion of real-time physics (see frame update diagram). This means although many physics engines need not be extensible from their parent game engine or even recognised as a separate software module. Consequently in this section we outline notable 3D real-time physics engines used in modern game engines for reference in later discussion. These range from open source to proprietary as well as some which are non-separable from their parent game engine.
NVIDIA PhysX
You may even recognise it from all those game packages – colloquially shortened to PhysX, NVIDIA PhysX is considered the most prolific physics engine within the game development community. Numerous games engine’s utilise PhysX such as Unity, Unreal Engine and Open 3D Engine. This traction has come from its rich feature set, high accuracy physics, strong CPU/GPU optimisations, large community and widely-permissible licensing. The engine itself is lightweight and flexible and is therefore seeing increasing use in tangential domains such as high-fidelity robotics simulation, medical simulation and scientific visualisation applications.
Havok Physics
Havok Physics is a proprietary physics engine used across many proprietary game engines such as Valve’s Source Engine, Ubisoft’s AnvilNext Engine, Electronic Art’s Frostbite Engine, Activision’s IW Engine and Unity. Havok Physics provides many of the same features as PhysX such as accurate rigid-body mechanics and hardware optimisations.
Bullet
Bullet is a free and fully open-source general-purpose physics engine that is increasingly being used as a alternative to the less actively maintained Open Dynamics Engine (ODE). With a python wrapper, Bullet is very much at the forefront of reinforcement learning and robotics simulation, used by countless researchers particularly in the field of quadrupedal robotics.
CryPhysics
CryPhysics is the physics engine used in Crytek’s game engine CryEngine. A notable example of its use has been The Climb, a game series where players attempt to scale massive structures like skyscrapers with movable handholds in VR and a personal favourite.
Notable Proprietary Physics Subsystems

Advanced VR Fluid Physics using Valve’s Rubikon Physics Engine in Half Life: Alyx
Unreal Engine’s Chaos Physics
Still in development, Unreal Engine’s Chaos Physics is a new lightweight physics engine slated to replace PhysX in future Unreal Engine releases. Chaos Physics has seen its debut in the popular online multi-player games like Fortnite, where it is being used as a testbed for high accuracy physics with many networked clients. Advancements over existing solutions include a faster physics solver, increased joint stability for ragdolls and integrated cloth mechanics.
Valve’s Rubikon
As part of Valve Corporation’s Source 2 game engine, Valve have been developing their in-house Rubikon physics engine. Currently unavailable to the public, more implementation specifics are expected with the general release of Source 2. This engine saw its debut in the milestone VR game Half Life: Alyx, providing quick update loops and high accuracy rigid-body physics with additional support for fluid and body-coupling mechanics.
This post was inspired by a recent review I did concerning the future of physics engines in the context of mixed reality: Physics Engines for Future VR